查询执行
查询执行
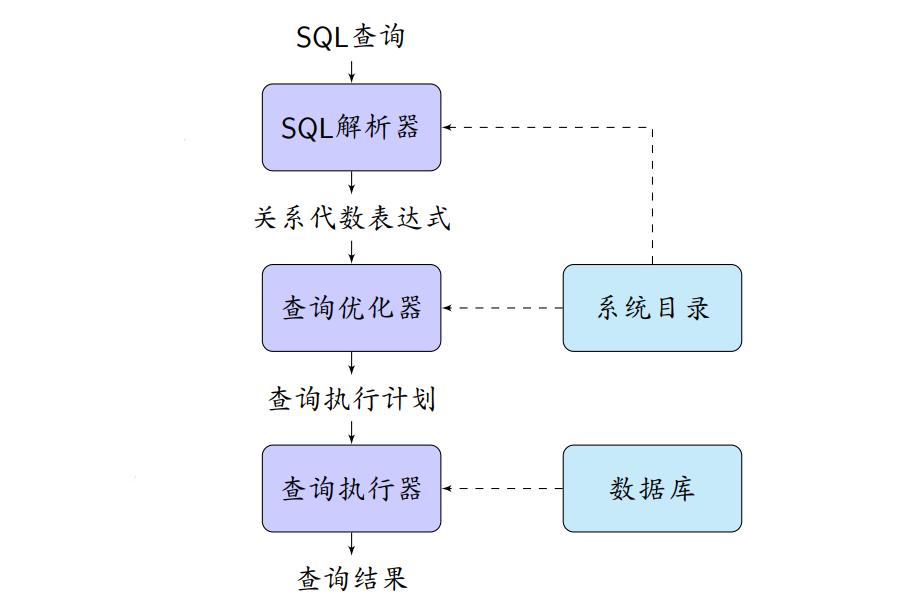
1. 概述
- SQL解析器
- SQL —> 计划
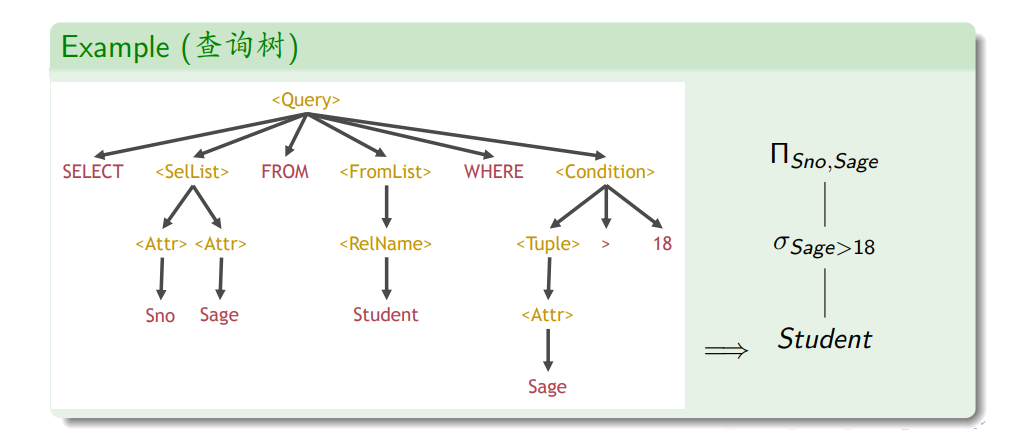
- 将一个SQL查询转换成关系代数表达式
- 查询优化器
- 初始计划 —> 估计代价最低的计划
- 将一个关系代数表达式转换成一个执行效率最高的等价关系代数表达式，并最终转换为查询执行计划
- 原语操作是带有“如何执行”注释的关系代数操作
- 查询执行计划是用于执行一个查询的原语操作序列
- 查询执行器
- 计划 —> 结果
2. 查询解析
词法分析
参考编译原理的词法分析
- 从左至右扫描SQL语句
- 产生token序列
- 词法分析器lex
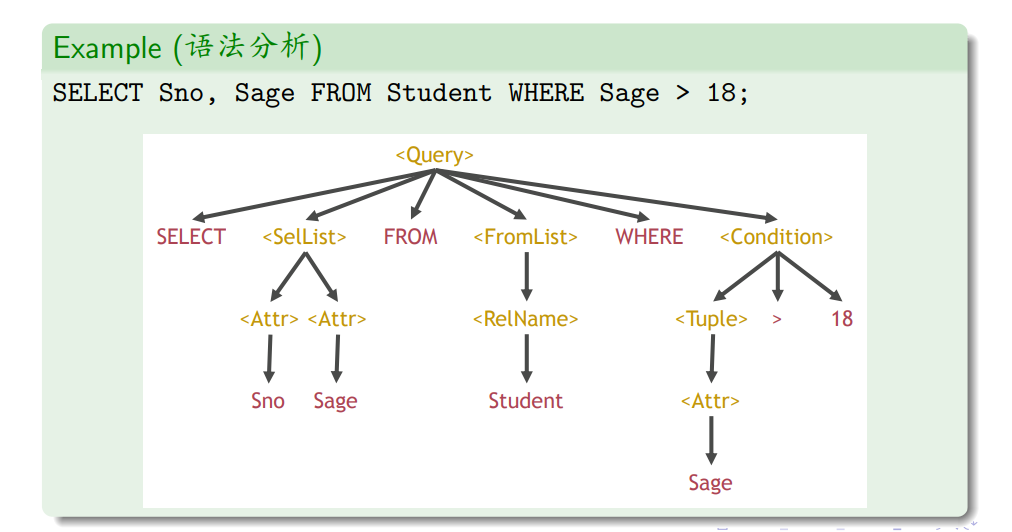
语法分析
参考编译原理的语法分析
- 将token序列转换成一棵抽象语法树（AST）
- 语法分析器yacc
语义分析
参考编译原理的语义分析
- 检查关系是否存在
- 检查属性是否存在
- 检查数据类型
- 检查访问权限
- 构造一棵查询分析树
3. 外排序
当数据规模大到无法全部载入内存时，需要使用外排序算法
外存归并
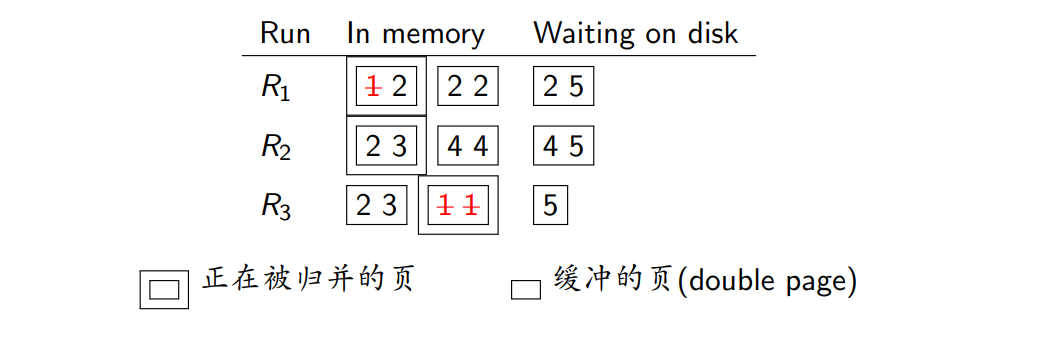
两趟多路外存归并排序
- 创建归并段
- 归并
多路归并
| 符号 | 说明 |
|---|---|
| $N$ | $R$的元组数 |
| $M$ | 缓冲池中可用内存页数 |
| $B$ | 每块最多存$B$个元组 |
| $B(R)$ | $R$的块数$\lceil N/B\rceil$ |
- 创建归并段
- 将关系$R$划分为$\lceil B(R)/M \rceil$个归并段
- 归并段内元组排序
- 合并
- 将$\lceil B(R)/M \rceil$个归并段中的元组进行归并
- 算法分析
- I/O代价：$3B(R)$
- 可用内存页数要求：$B(R)\leq M^2$
- 每个归并段不超过M页
- 最多M个归并段
多趟多路外存归并排序
- 若$B(R) > M^2$，则需要执行多趟多路外存归并排序
- I/O代价为$(2m-1)B(R)$，其中m为算法执行的趟数
双缓冲
- 为每个归并段分配多个内存页作为输入缓冲区
- 在当前缓冲页中所有元组都已归并完毕时，DBMS直接开始归并下一缓冲页中的元组
- 与此同时，DBMS将归并段文件的下一块读入空闲的缓冲页
4. 关系代数运算的执行
（1）选择操作
| 符号 | 说明 |
|---|---|
| $T(R)$ | 关系$R$的元组数 |
| $B(R)$ | 关系$R$的块数 |
| $M$ | 缓冲池中可用内存页数 |
| $V(R,A)$ | 关系$R$的属性集$A$的不同值的个数 |
a. 基于扫描的选择算法
1
2
3
4
5
for R中的每一块P do
将P读入缓冲池
for P中每条元组t do
if t满足选择条件 then
将t写入输出缓冲区
- 算法分析
| 类型 | 值 |
|---|---|
| I/O代价 | $B(R)$ |
| 可用内存 | $M\geq 1$ |
b. 基于哈希的选择算法
- 前提条件
- 关系R采用哈希文件组织形式
- 选择条件的形式是$K = v$，属性$K$是R的哈希键 ```
- 根据hash(v)确定结果元组所在的桶
- 在桶页面中搜索键值等于v的元组，并将元组写入输出缓冲区 ```
- 算法分析
| 类型 | 值 |
|---|---|
| I/O代价 | $\lceil B(R)/V(R,K)\rceil$ |
| 可用内存 | $M\geq 1$ |
c. 基于索引的选择算法
- 前提条件
- 选择条件的形式是$K=v$或$I\leq K \leq u$
- 关系R上建有属性K的索引
- 在索引上搜索满足选择条件的元组，并将元组写入输出缓冲区
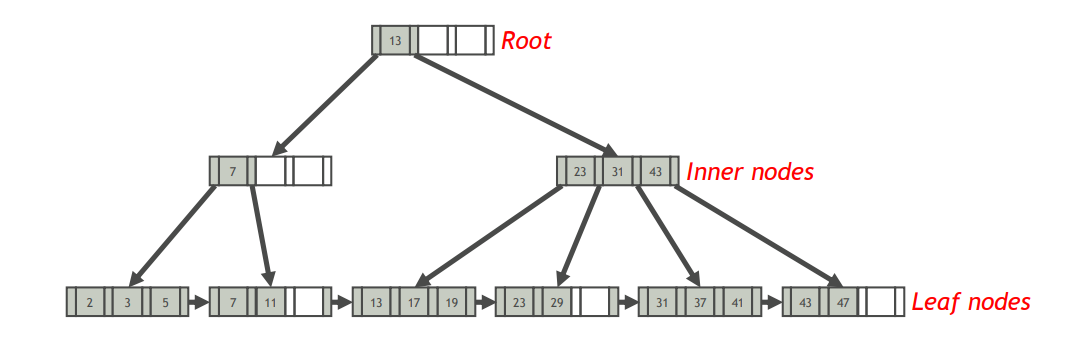
- 算法分析
- 若索引是聚簇索引
- 结果元组连续存储于文件中
类型 值 I/O代价 $\lceil B(R)/V(R,K)\rceil$ 可用内存 $M\geq 1$ - 若索引是非聚簇索引
- 结果元组不一定连续存储于文件中
类型 值 I/O代价 $\lceil T(R)/V(R,K)\rceil$ 可用内存 $M\geq 1$
（2）不带去重的投影算法
1
2
3
4
5
for R中的每一块P do
将P读入缓冲池
for P中每条元组t do
将t向投影属性集做投影
将投影元组写入输出缓冲区
该算法在数据访问模式上与基于扫描的选择算法相同
（3）去重操作
a. 一趟去重算法
1
2
3
4
5
for R中的每一块P do
将P读入缓冲池
for P中每条元组t do
if 未见过t then
将t写入输出缓冲区
- 在可用内存页中用哈希表记录见过的元组，哈希键为整个元组
- 算法分析
类型 值 I/O代价 $B(R)$ 可用内存 $B(\delta(R))\leq M-1$
R中互不相同的元组$\delta(R)$必须能在$M-1$页中存得下
b. 基于排序的去重算法
- 与多路归并排序算法本质上一样
- 在创建归并段时，按整个元组进行排序
- 在归并阶段，相同元组只输出1个，其他全部丢弃
- 算法分析
类型 值 I/O代价 $3B(R)$ 可用内存 $B(R)\leq M^2$
c. 基于哈希的去重算法
1
2
3
4
5
6
7
8
// 哈希分桶
for R的每一块P do
将P读入缓冲池
将P中元组哈希到M-1个桶R1,R2,..,R(M-1)中（哈希键为整个元组）
//逐桶去重
for i = 1,2,...,M-1 do
在桶Ri上执行一趟去重算法，并将结果写到输出缓冲区
- 算法分析
类型 值 I/O代价 $3B(R)$ 可用内存 $B(R)\leq (M-1)^2$
（4）集合差操作
a. 一趟集合差算法
1
2
3
4
5
6
7
8
9
10
11
12
//构建阶段
在M-1个可用内存页中建立一个内存查找结构（哈希表或平衡二叉树），查找键是整个元组
for S的每一块P do
将P读入缓冲池
将P中元组插入内存查找结构
// 探测阶段
for R的每一块P do
将P读入缓冲池
for P中每条元组t do
if t不在于内存查找结构中 then
将t写入输出缓冲区
- 算法分析
类型 值 I/O代价 $B(R)+B(S)$ 可用内存 $B(S)\leq M-1$ - 内存查找结构约占$B(S)$页
b. 基于哈希的集合差算法
1
2
3
4
5
6
7
// 哈希分桶（与基于哈希的去重算法的分桶方法相同）
将R的元组哈希到M-1个桶R1,R2,...,R(M-1)中（哈希将为整个元组）
将S的元组哈希到M-1个桶S1,S2,...,S(M-1)中（哈希键为整个元组）
// 逐桶计算集合差
for i = 1,2,...,M-1 do
使用一趟集合差算法计算Ri-Si，并将结果写入输出缓冲区
- 算法分析
类型 值 I/O代价 $3B(R)+3B(S)$ 可用内存 $B(S)\leq (M-1)^2$
c. 基于排序的集合差算法
1
2
3
4
5
6
7
8
9
10
11
12
13
// 创建归并段
将R划分为B(R)/M（向上取整）个归并段（每个归并段按整个元组进行排序）
将S划分为B(S)/M（向上取整）个归并段（每个归并段按整个元组进行排序）
// 归并
读入R和S的每个归并段的第1页
repeat
找出输入缓冲区中最小的元组t
if t属于R 且 t不属于S then
将t写入输出缓冲区
从输入缓冲区中删除t的所有副本
任意输出缓冲页中的元组若归并完毕，则读入其归并段的下一页
until R的所有归并段都已归并完毕
- 算法分析
类型 值 I/O代价 $3B(R)+3B(S)$ 可用内存 $B(R)+B(S)\leq M^2$
（5）连接操作
$R(X,Y) \Join S(Y,Z)$
a. 一趟连接算法
1
2
3
4
5
6
7
8
9
10
11
12
// 构建阶段
在M-1个可用内存页中建立一个内存查找结构（哈希表或平衡二叉树），查找键是S.Y
for S的每一块P do
将P读入缓冲池
将P中元组插入内存查找结构
// 探测阶段
for R的每一块P do
将P读入缓冲池
for P中每条元组r do
for 内存查找结构中每条键值等于r.Y的元组s do
连接r和s，并将结果写入输出缓冲区
- 算法分析
类型 值 I/O代价 $B(R)+B(S)$ 可用内存 $B(S)\leq M-1$
b. 嵌套循环连接
基于元组
1
2
3
4
for S中的每个元组s do
for R中的每个元组r do
if r和s满足连接条件 then
连接r和s，并将结果写入输出缓冲区
- 算法分析
类型 值 I/O代价 $T(S)(T(R)+1)$ 可用内存 $M\geq 2$
基于块
1
2
3
4
5
6
7
8
9
假设：B(S) <= B(R)
for 外关系S的每M-1块 do
将这M-1块读入缓冲池
用一个内存查找结构来组织这M-1块中的元组
for 内关系R的每一块P do
将P读入缓冲池
for P中每条元组r do
for 内存查找结构中能与r进行连接的元组s do
连接r和s，并将结果写入输出缓冲区
- 算法分析
类型 值 I/O代价 $B(S)+\frac{B(R)B(S)}{M-1}$ 可用内存 $M\geq 2$
c. 排序归并连接
1
2
3
4
5
6
7
8
9
10
11
12
13
// 创建归并段
将R划分为B(R)/M（向上取整）个归并段（每个归并段按R.Y排序）
将S划分为B(S)/M（向上取整）个归并段（每个归并段按S.Y排序）
// 归并
读入R和S的每个归并段的第1页
repeat
找出输入缓冲区中元组Y属性的最小值y
for R中满足R.Y=y的元组r do
for S中满足S.Y=y的元组s do
连接r和s，并将结果写入输出缓冲区
任意输出缓冲页中的元组若归并完毕，则读入其归并段的下一页
until R或S的所有归并段都已归并完毕
- 算法分析
类型 值 I/O代价 $3B(S)+3B(S)$ 可用内存 $B(R)+B(S)\leq M^2$
d. Grace哈希连接
1
2
3
4
5
6
7
// 哈希分桶
将R的元组哈希到M-1个桶（哈希键为R.Y）
将S的元组哈希到M-1个桶（哈希键为S.Y）
// 逐桶连接
for i = 1,2,...,M-1 do
使用一趟连接算法计算Ri /Join Si，并将结果写入输出缓冲区
- 算法分析
类型 值 I/O代价 $3B(S)+3B(S)$ 可用内存 $B(S)\leq (M-1)^2$
e. 索引连接
1
2
3
4
5
6
7
假设：关系S上建有属性Y的索引
for R中的每一块P do
将P读入缓冲区
for P中每条元组r do
在索引上查找键值等于r.Y的S的元组集合T
for s 属于 T do
连接r和s，并将结果写入输出缓冲区
- 算法分析
- 若索引是非聚簇索引
类型 值 I/O代价 $B(R)+\frac{T(R)T(S)}{V(S,Y)}$ 可用内存 $M\geq 2$ - 若索引是聚簇索引
类型 值 I/O代价 $B(R)+T(R)\lceil \frac{B(S)}{V(S,Y)} \rceil$ 可用内存 $M\geq 2$
5. 查询计划的执行方法
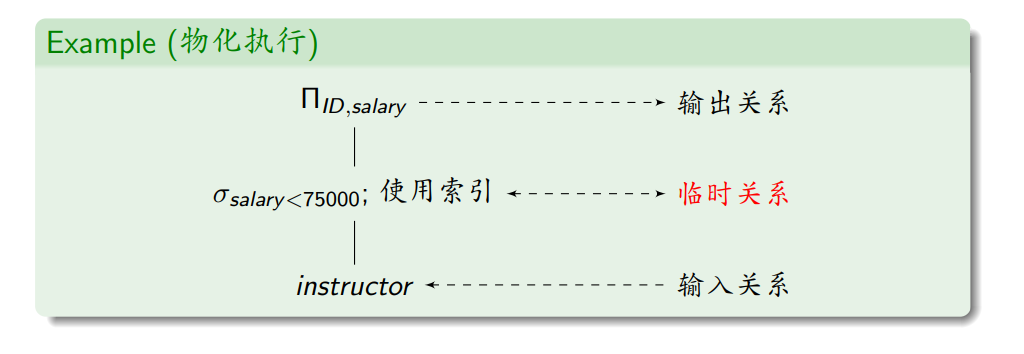
（1）物化执行
- 自底向上执行查询计划中的操作
- 每个中间操作的执行结果写入临时关系文件，作为后续操作的输入
（2）流水线执行(piplining) / 火山模型(the volcano model)
- 将查询计划中若干操作组成流水线，一个操作的结果直接传给流水线中下一个操作
- 避免产生一些临时关系，避免了读写这些临时关系文件的I/O开销
- 用户能够尽早得到查询结果
This post is licensed under CC BY 4.0 by the author.