索引结构
索引结构
1. 索引分类
- 按照索引的实现方式
- 有序索引
- 通过索引键有序排列索引项来实现索引
- 哈希索引
- 通过按索引键哈希值分桶来实现索引
- 有序索引
有序索引
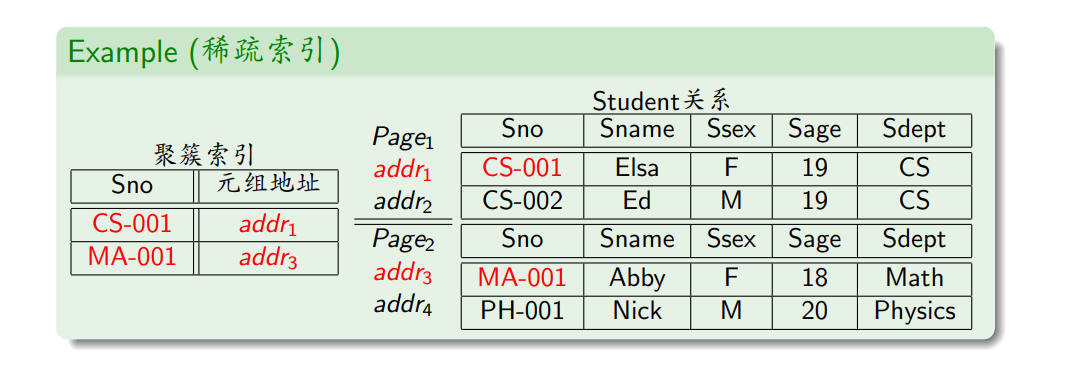
- 按照数据文件的元组是否按索引键排序
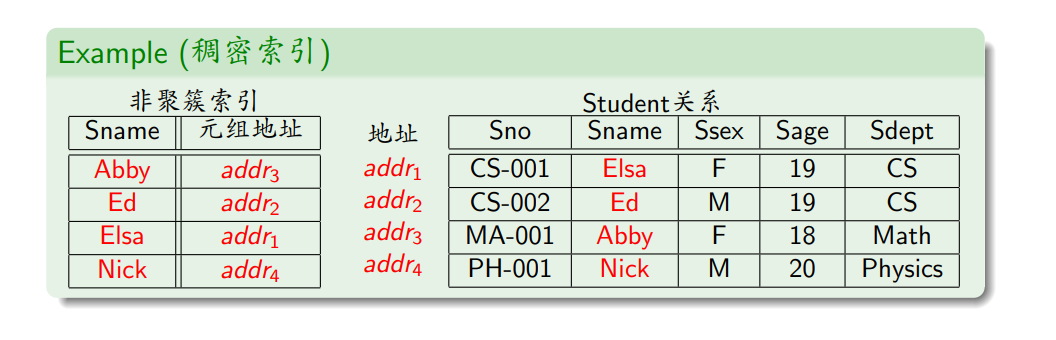
- 根据关系中每个元组在索引中是否都有一个对应的索引项
- 根据索引键是否为关系的主键
- 主索引
- 索引键是关系的主键
- 一个关系只有一个主索引
- 二级索引
- 索引键不是关系的主键
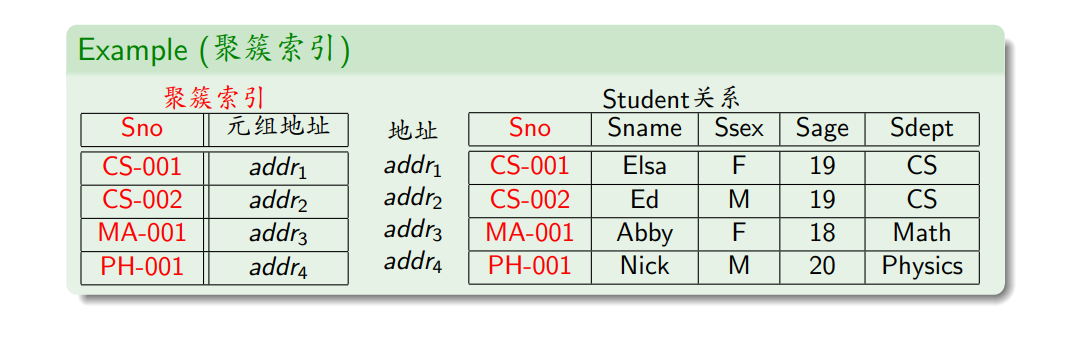
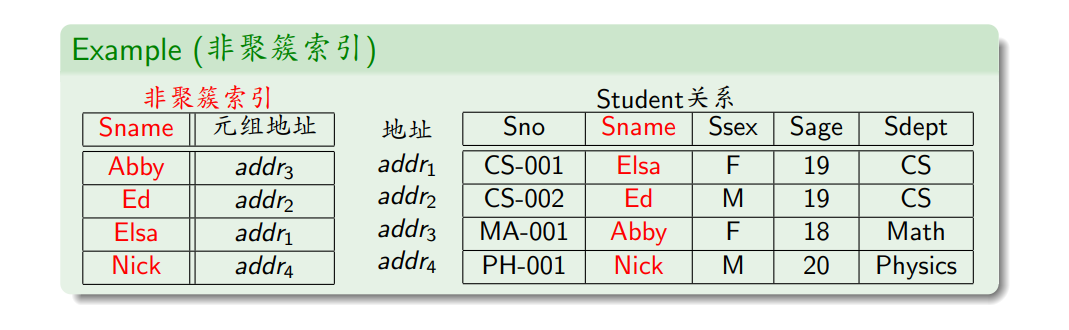
- 通常是非聚簇索引
- 一个关系可以有多个二级索引
- 主索引
- 唯一索引
- 索引键值不能重复
- 主索引一定是唯一索引
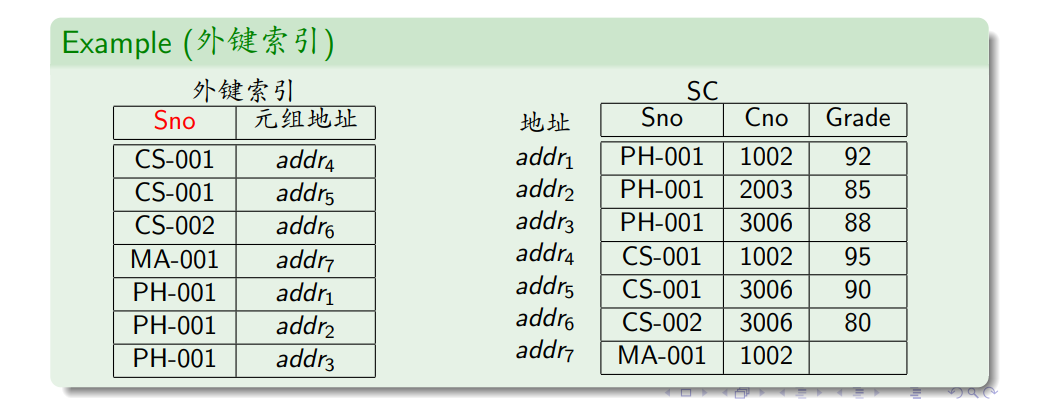
- 外键索引
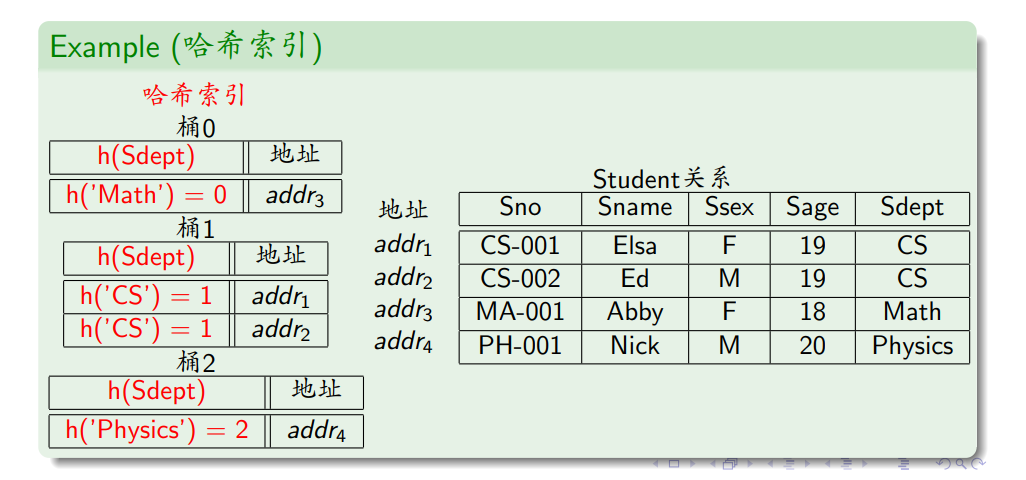
哈希索引
2. 索引结构
- 有序索引的数据结构
- 平衡树
- 跳表(skiplist):多用于内存数据库系统
- 字典树(trie):多用于内存数据库系统
- 日志结构合并树(LSM-Tree):多用于NoSQL数据库系统的存储引擎
- 哈希索引的数据结构
- 哈希表
3. 哈希索引结构
外存哈希表
- 键为K的索引项属于编号为hash(K)的桶
- 每个桶中存放一个指针,指向存储该桶中索引项的页
- 分类
- 静态哈希表
- 桶的数量固定不变
- 动态哈希表
- 桶的数量动态变化,使每个桶中的索引项存储在大约1个页中
- 可扩展哈希表
- 线性哈希表
- 静态哈希表
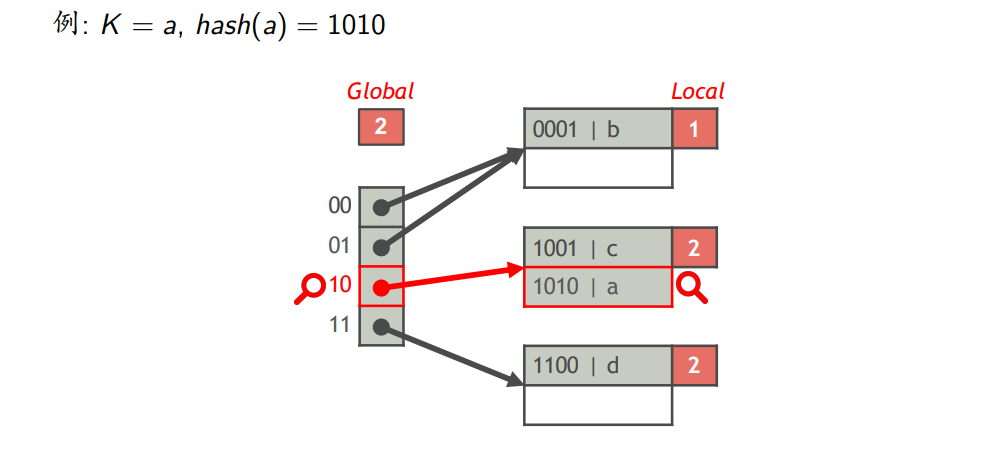
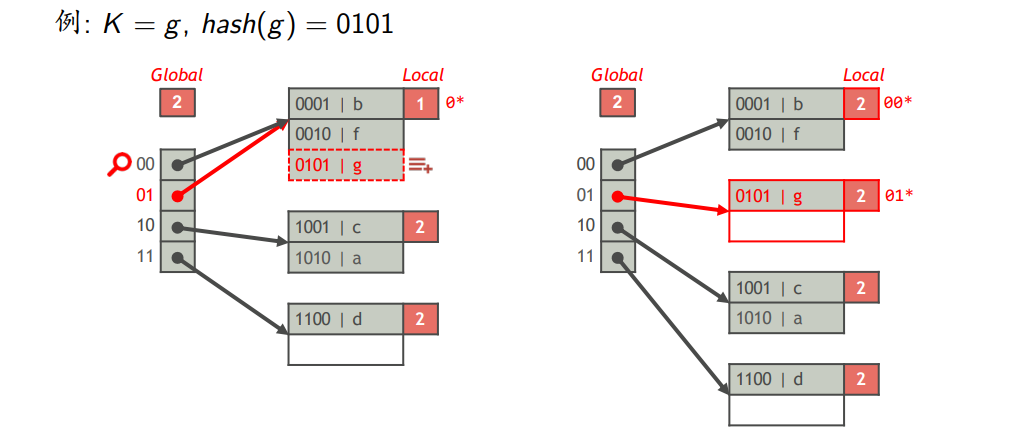
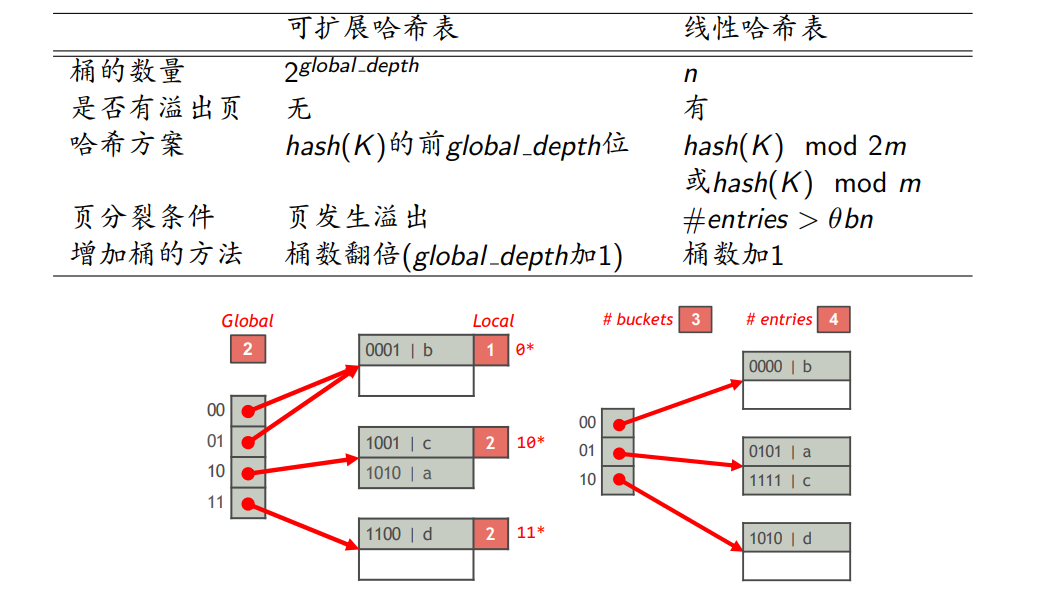
(1)可扩展哈希表
- 全局深度(i)
- hash(K)的前i位相同的索引项放在同一个桶中
- 一个可扩展哈希表包含$2^i$个桶
- 每个页记录一个局部深度j,该页中的全部索引项的hash(K)的前j位相同,用于标识这些索引项都存于这个页
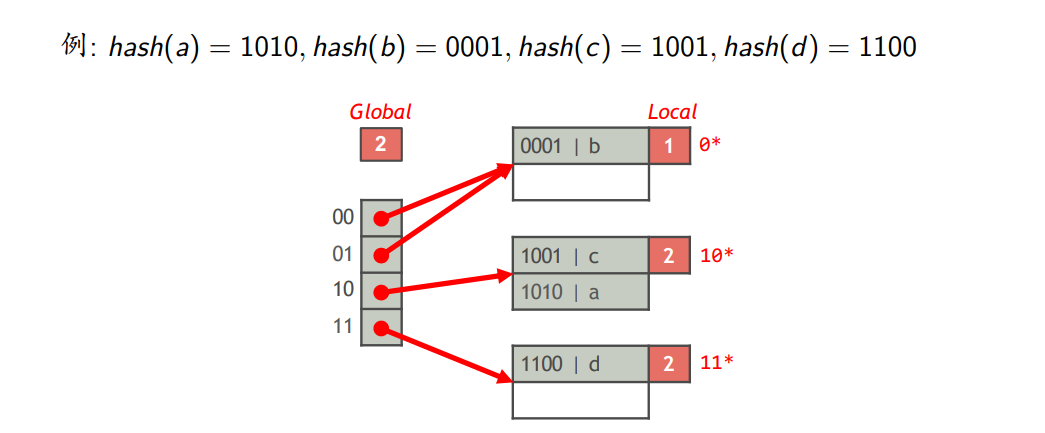
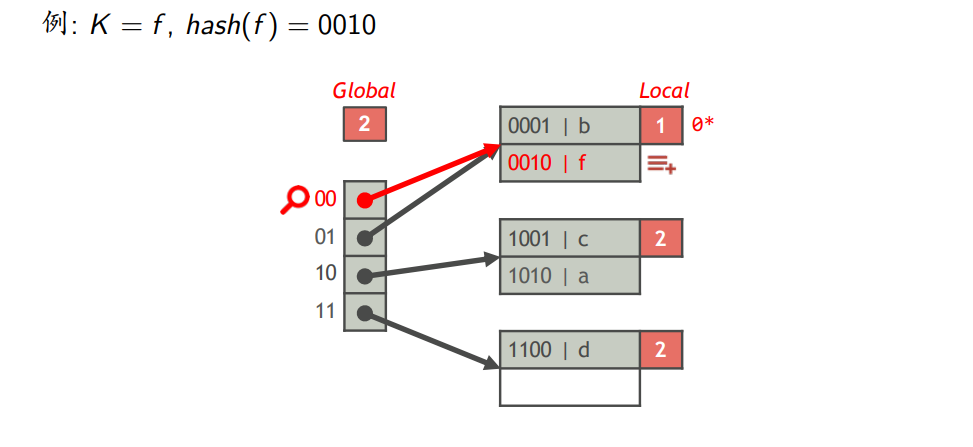
- 查找索引项
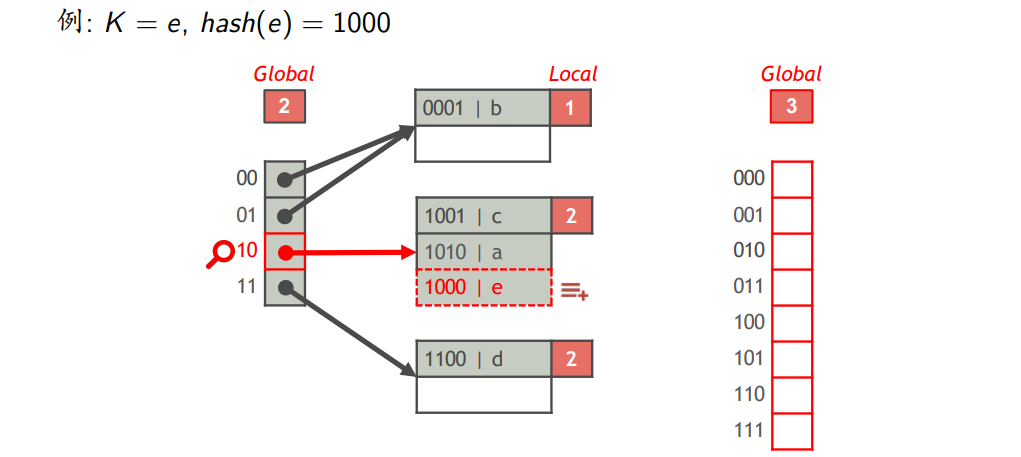
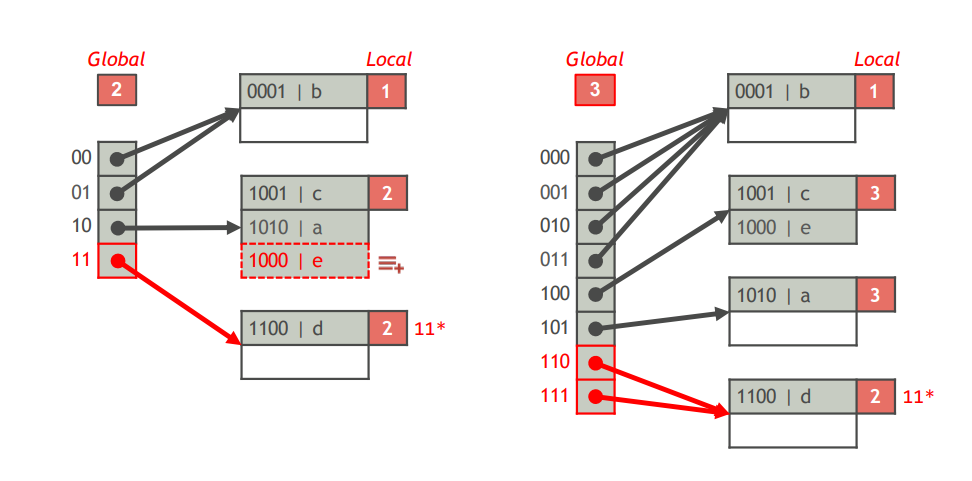
- 插入索引项
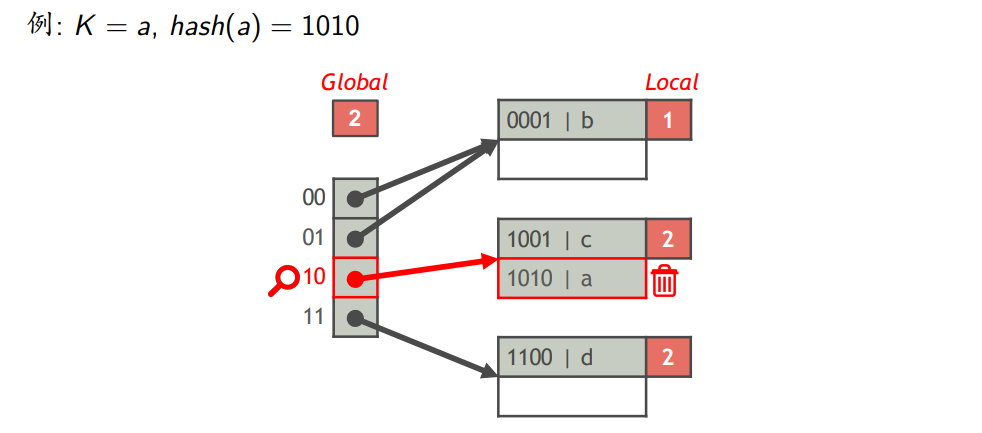
- 删除索引项
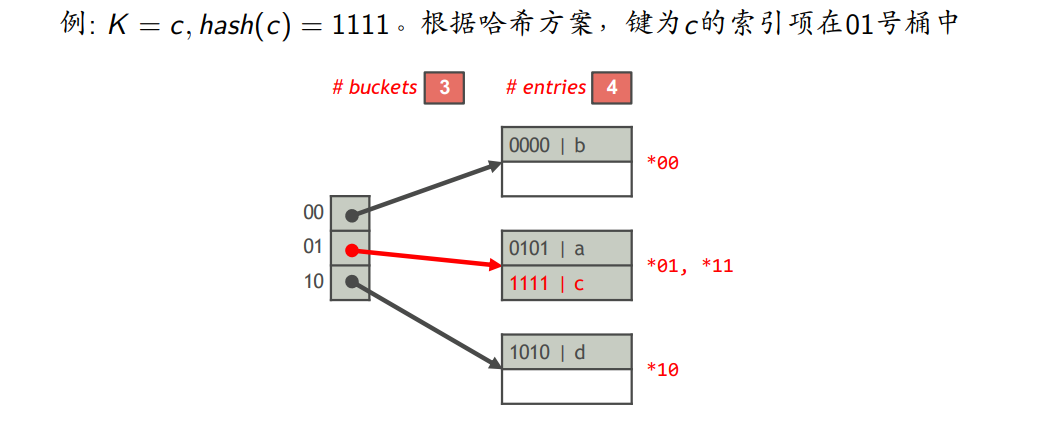
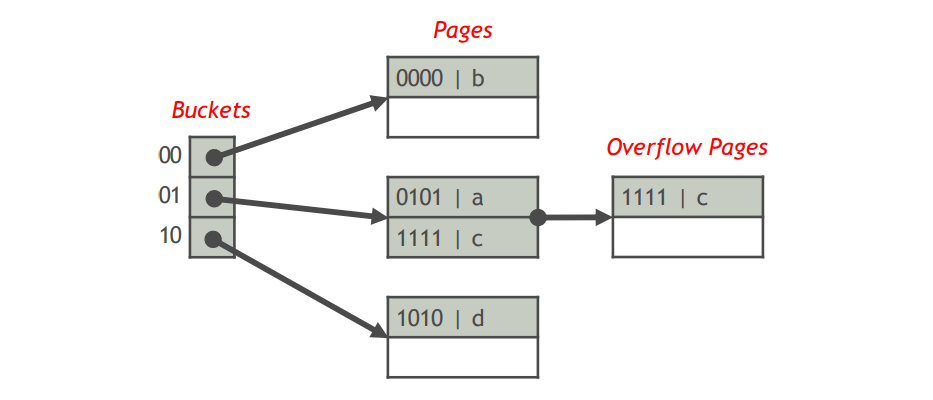
(2)线性哈希表
- 包含$n$个桶,每个桶只有一个页,每个页最多存储$b$个索引项,则线性哈希表中最多存储$\theta bn$个索引项,其中$0<\theta <1$是一个阈值
- 记录线性哈希表中桶的数量和索引项的数量
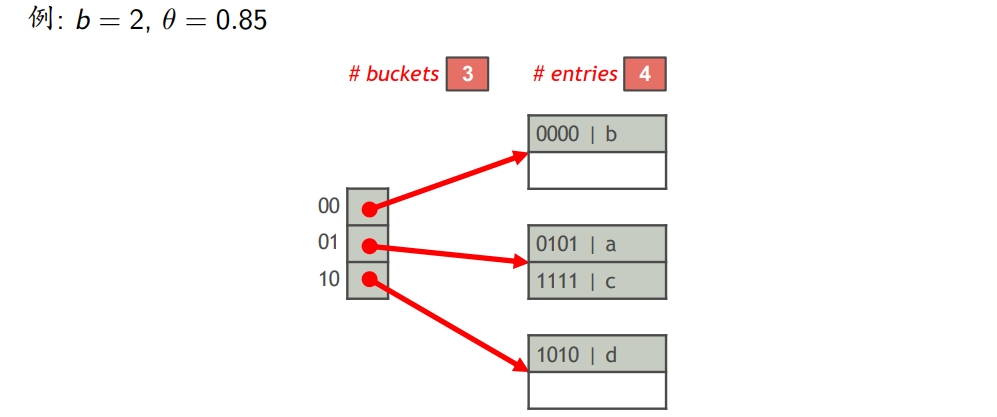
- 哈希方案描述
- 桶号$0,1,…,n-1$
- $m=2^{\lfloor log_2n \rfloor},m\leq n <2m$
编号K 该索引项属于的桶 $hash(K)~~mod~2m < n$ 编号为$hash(K)~~mod~2m$的桶 $\geq$ 编号为$hash(K)~~mod~m$的桶
- 查找索引项
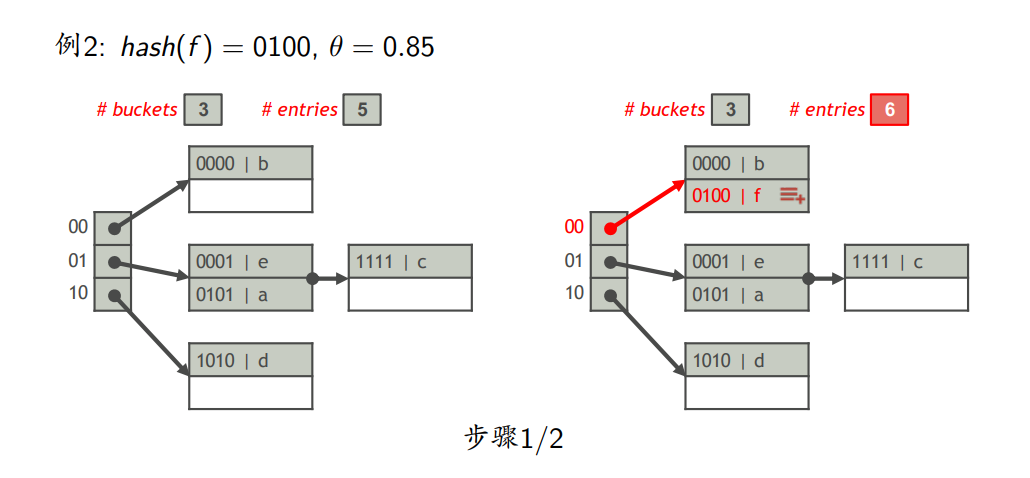
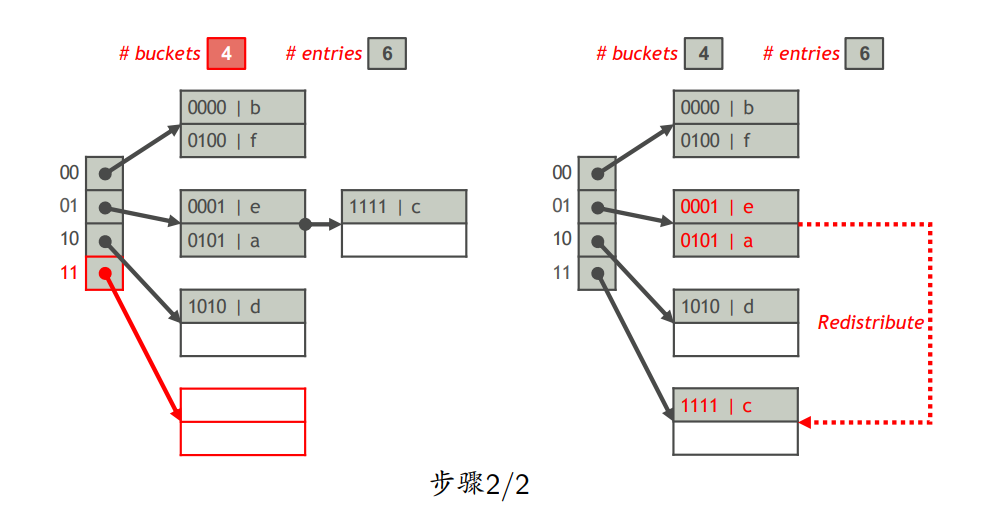
- 插入索引项
- 线性散列比可扩展动态散列更灵活;但如果数据散列后分布不均匀,导致的问题可能会比可扩展散列还严重。
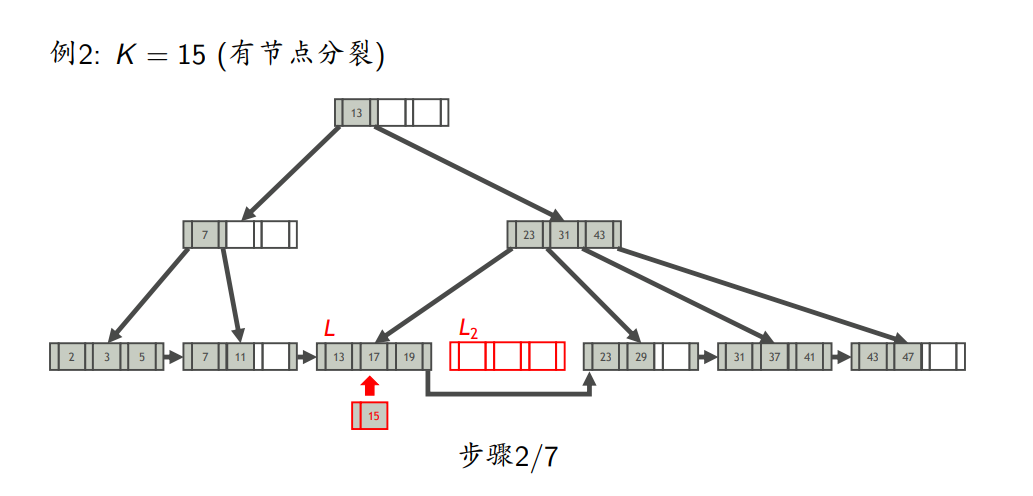
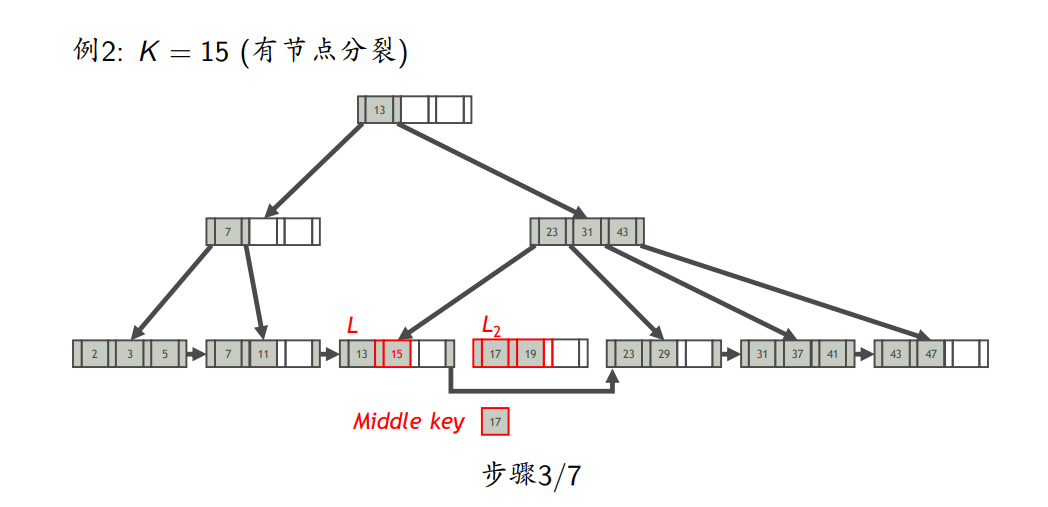
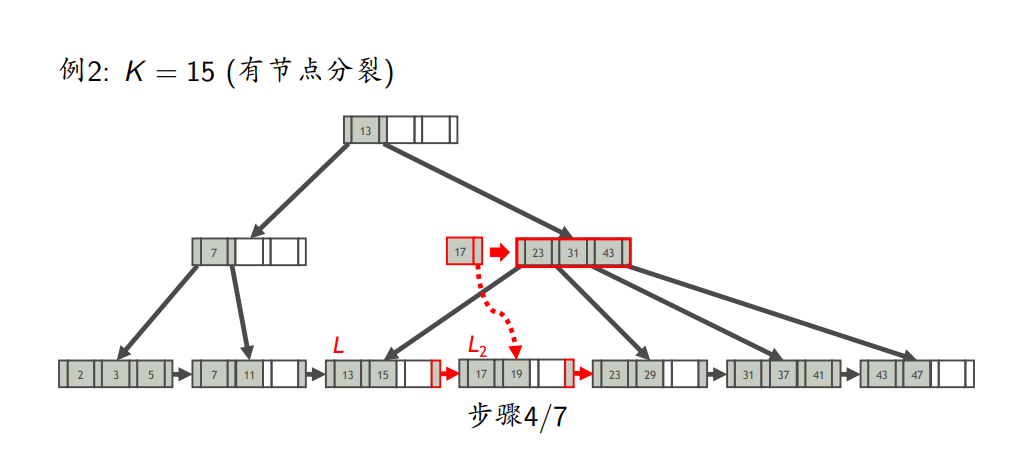
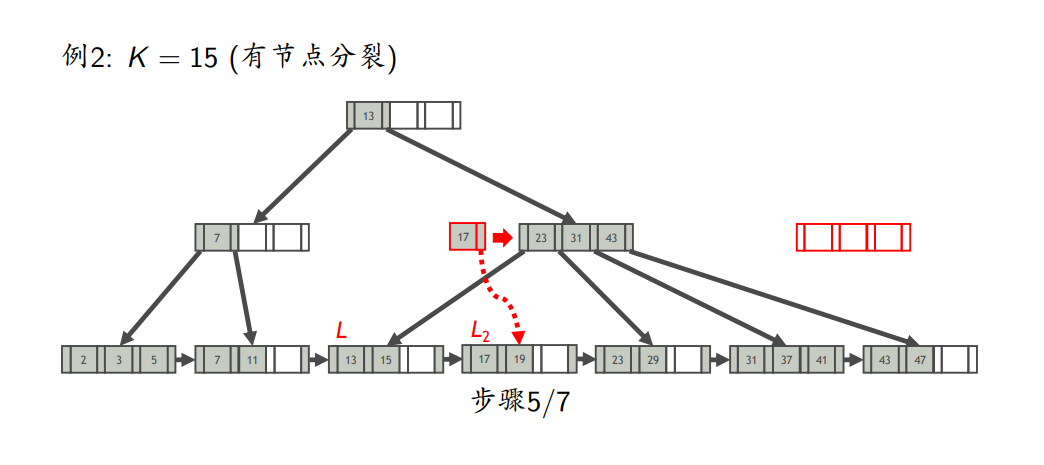
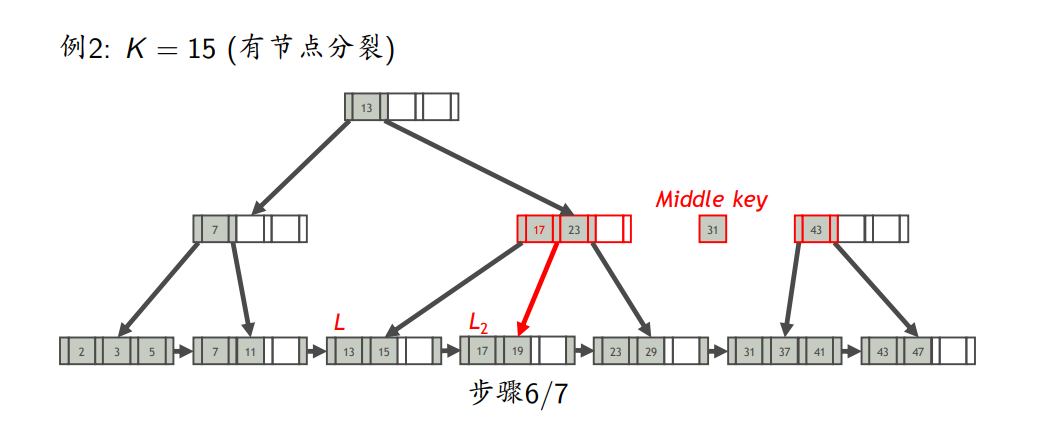
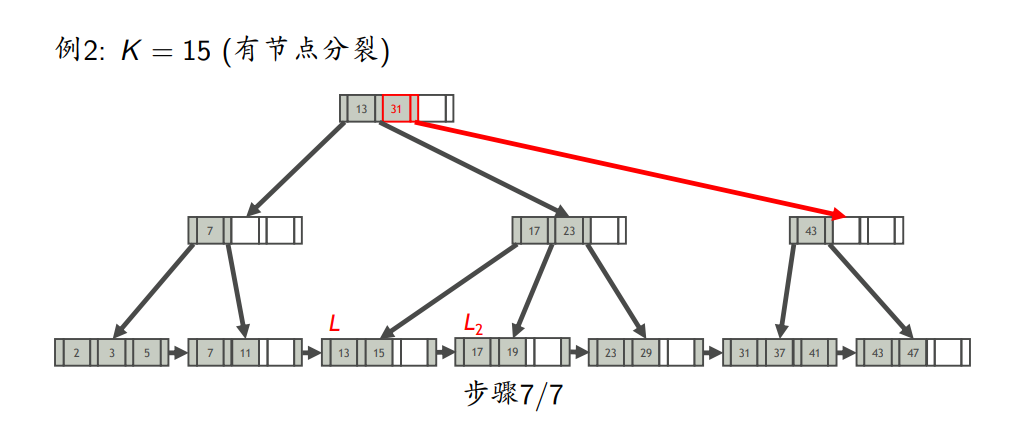
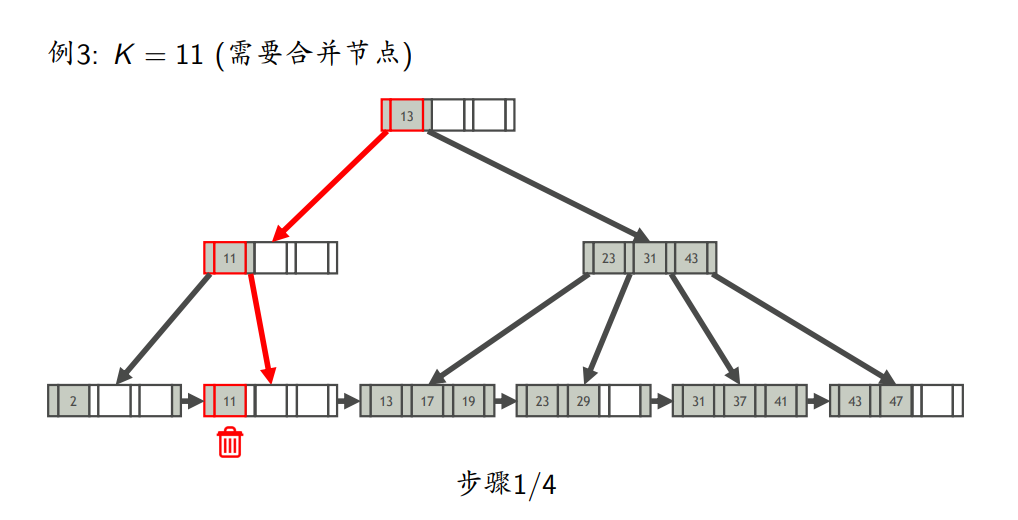
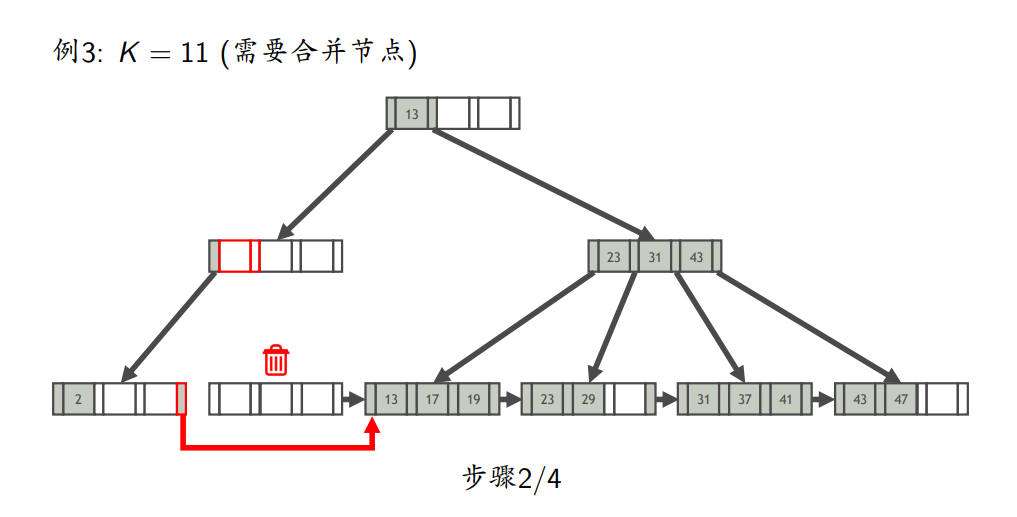
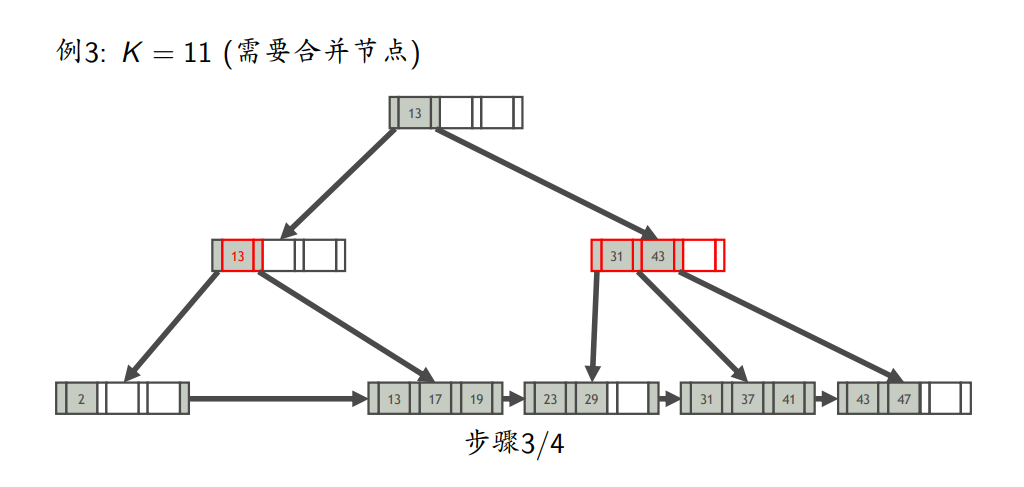
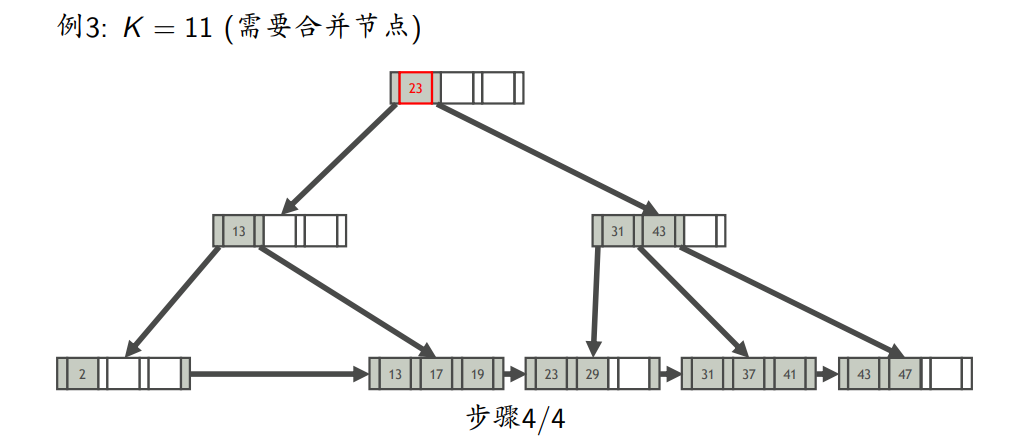
4. 树索引结构
B+树
- B+树是一棵M路平衡搜索树
数据结构
- 所有叶节点都在同一层上
- 除根节点外,每个节点至少“半满”,即$\frac{M}{2}-1\leq keys\leq M-1$
- 每个节点恰好放入1个页
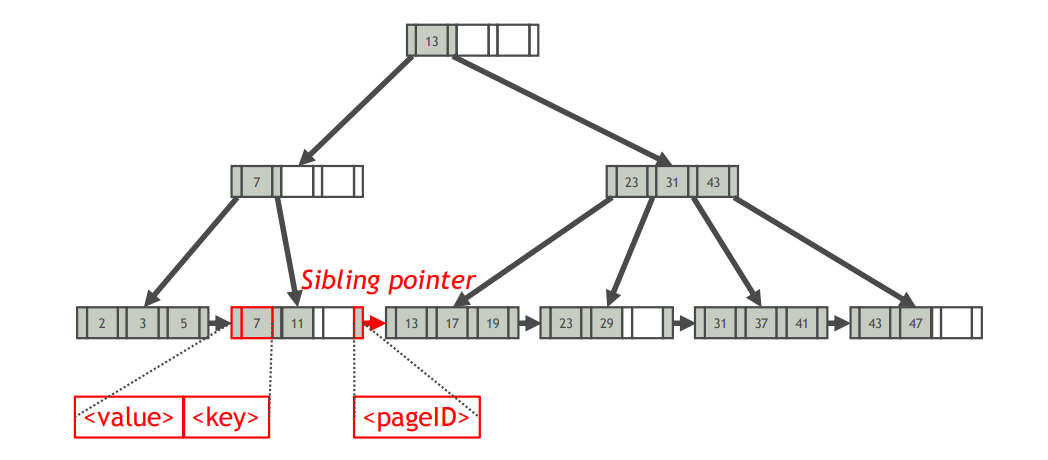
- 叶节点
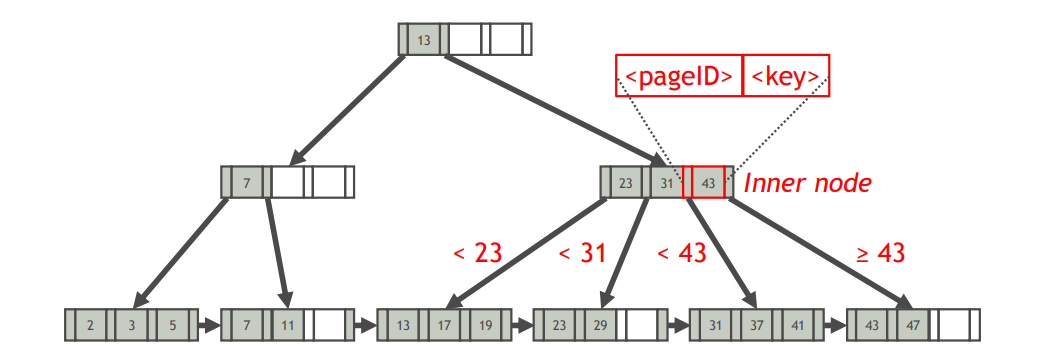
- 内节点
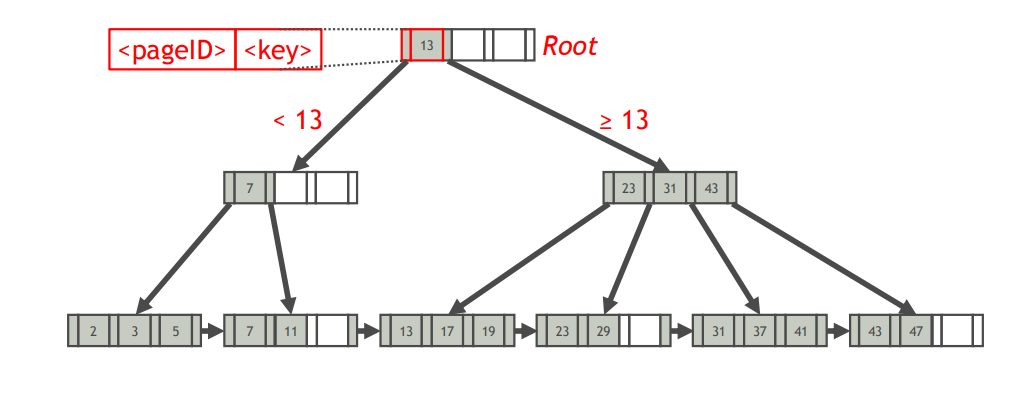
- 根节点
操作
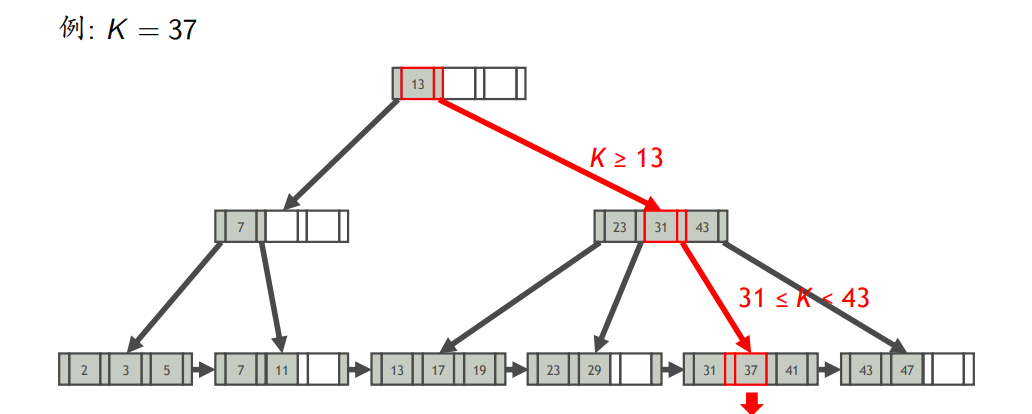
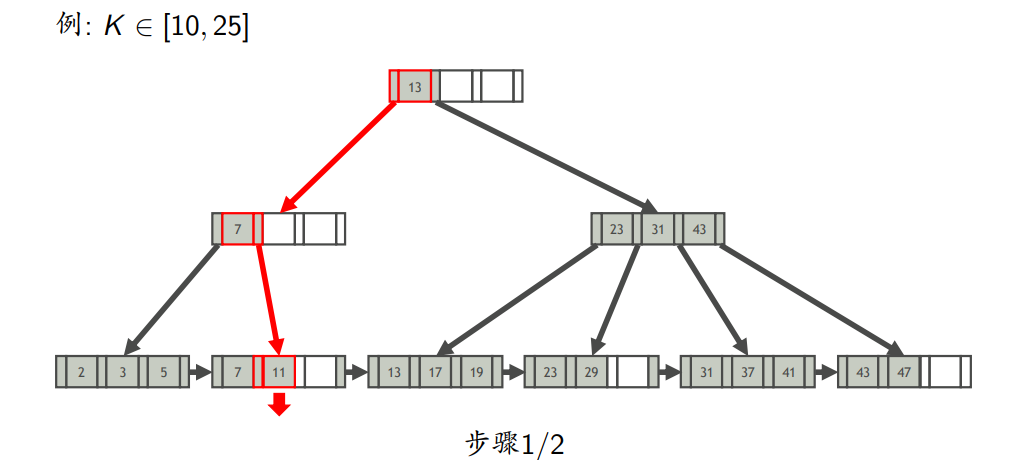
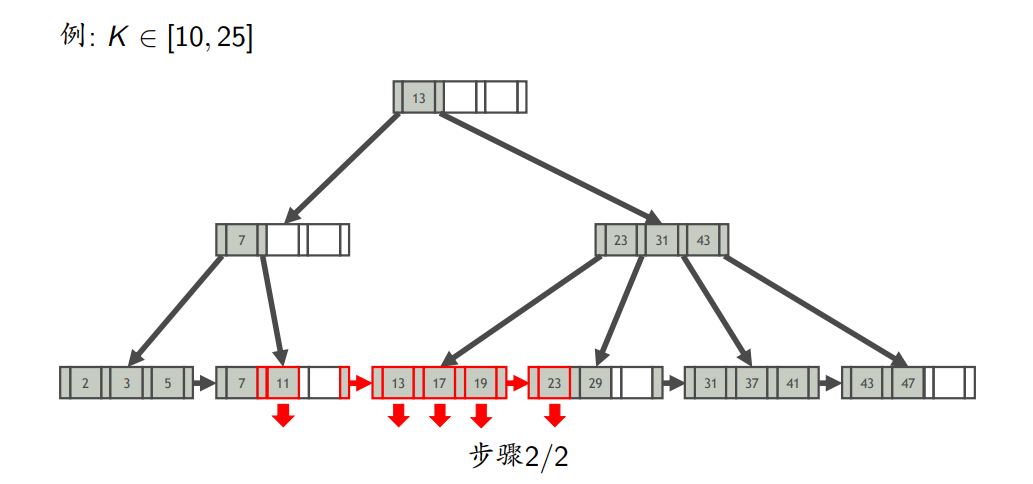
- 查找
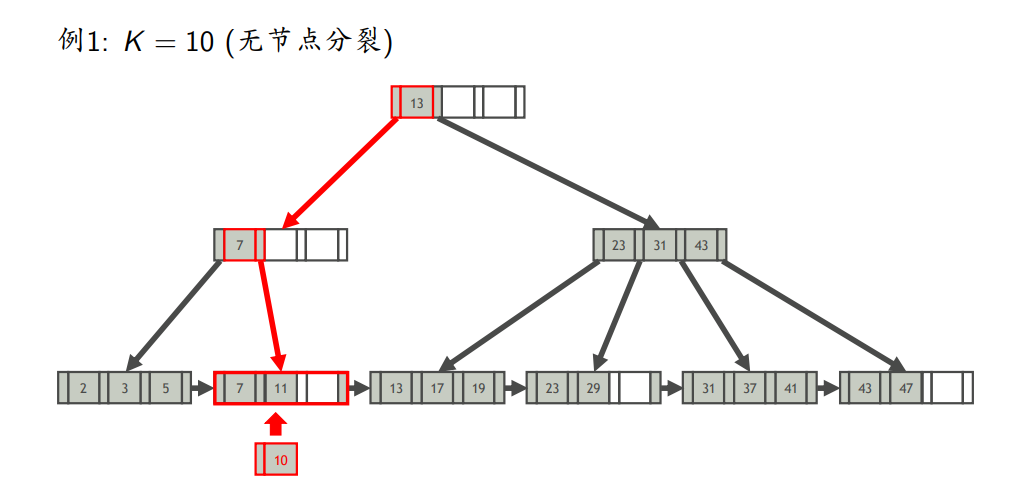
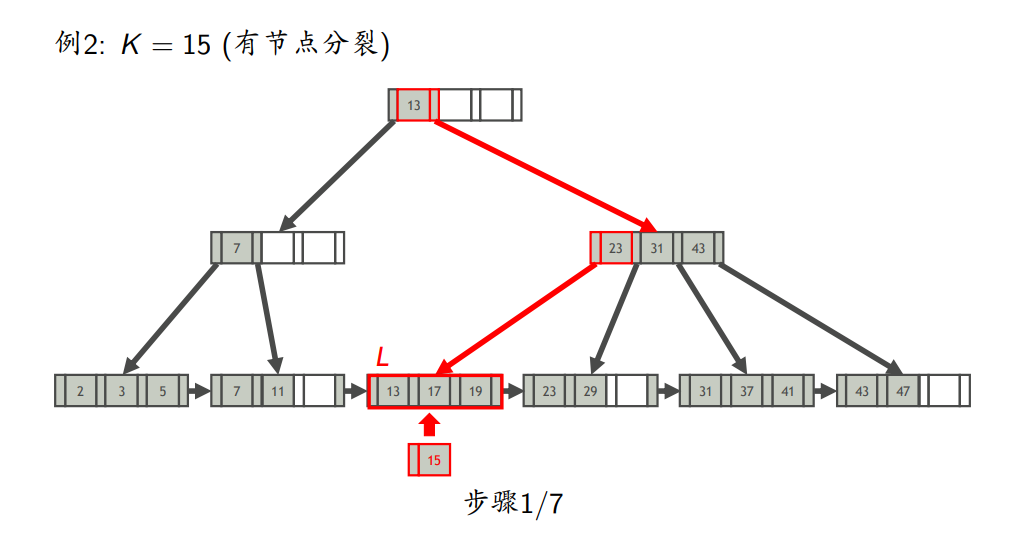
- 插入
- 删除
键压缩
从B+树中查找一个索引项所需的磁盘I/O数 = B+树的高度
- 扇出数:一个节点所能拥有的子节点的最大数量
- 较大的扇出数通常意味着树的高度相对较小,因为更多的子节点可以存储在一个节点中,减少整棵树的高度,从而减少了磁盘I/O的次数
- 索引键越长–> 扇出数越小–>B+树越高–>查询时间越长
所以应该尽可能减小索引键的长度
- 前缀压缩
- 后缀截断
This post is licensed under CC BY 4.0 by the author.