计算机的运算方法
计算机的运算方法
3.1 无符号数和有符号数
无符号数
- 寄存器的位数(n)反映无符号数的表示范围:$0$~$2^n-1$
有符号数
机器数与真值
真值 机器数 +0.1011 0.1011 -0.1011 1.1011 +1100 0,1100 -1100 1,1100 实际表示并不存在小数点和逗号
原码表示法
- 整数表示 \([x]_原 =\begin{cases} 0,x & 2^n>x \geq 0 \\ 2^n-x & 0 \geq x > -2^n \end{cases}\)
- 小数表示 \([x]_原 =\begin{cases} x & 1>x \geq 0 \\ 1-x & 0 \geq x > -1 \end{cases}\)
- 0的原码
补码表示法
- 整数表示 \([x]_补 =\begin{cases} 0,x & 2^n>x \geq 0 \\ 2^{n+1}+x & 0 > x \geq -2^n \end{cases}\)
- 小数表示 \([x]_补 =\begin{cases} x & 1>x \geq 0 \\ 2+x & 0 > x \geq -1 \end{cases}\)
- 原码与补码的快速转换(转换一致) 对于负数而言,除符号位外,每位取反,末位加1
- 由$[y]_补$求$[-y]_补$:每位取反,末位加1
反码表示法
- 整数 \([x]_反 =\begin{cases} 0,x & 2^n>x \geq 0 \\ (2^{n+1}-1)+x & 0 \geq x > -2^n \end{cases}\)
- 小数 \([x]_反 =\begin{cases} x & 1>x \geq 0 \\ (2-2^{-n})+x & 0 \geq x > -1 \end{cases}\)
- 总结:除符号位外,每位取反
移码表示法
$[x]_移 = 2^n+x (2^n>x \geq -2^n)$
- 移码和补码只差一个符号位 (对于同一个真值)
3.2 数的定点表示和浮点表示
定点表示
定点数:小数点固定在某一位置的数
数 说明 纯小数 小数点位于数符和第一数值之间 纯整数 小数点位于数值位之后 定点机:采用定点数的机器
定点机 小数定点机 整数定点机 原码 $-(1-2^{-n}) \sim +(1-2^{-n})$ $-(2^{n}-1) \sim +(2^{n}-1)$ 补码 $-1 \sim +(1-2^{-n})$ $-2^{n} \sim +(2^{n}-1)$ 反码 $-(1-2^{-n}) \sim +(1-2^{-n})$ $-(2^{n}-1) \sim +(2^{n}-1)$
浮点表示
- 浮点数:小数点位置可以浮动的数
- $N=S\times r^j$
- S尾数:小数,可正可负
- j阶码:整数,可正可负
- r基数:2、4、8、16等
- 表示
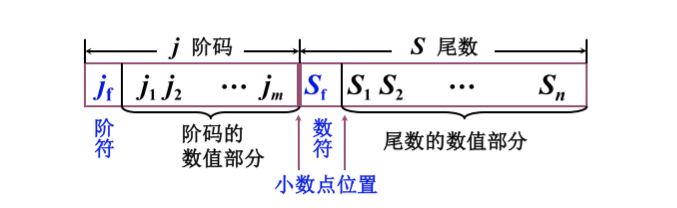
- n:反映浮点数的精度
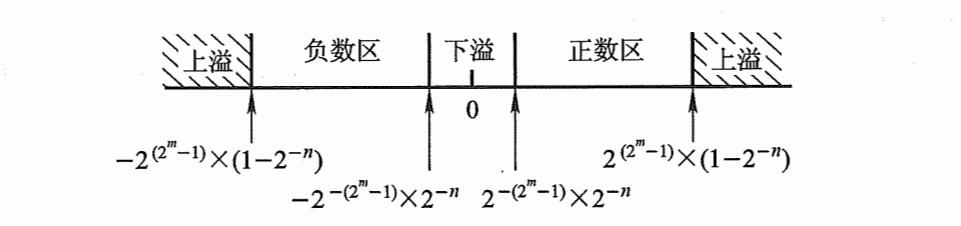
- m:反映浮点数的表示范围
事件 解释 处理 上溢 阶码>最大阶码 机器停止运算,进行中断溢出处理 下溢 阶码<最小阶码 按机器零处理,机器继续运行 - 规格化
基数 规格化数 r=2 尾数最高位为1 r=4 尾数最高位2位不全为0 r=8 尾数最高位3位不全为0 - 基数r越大,可表示的浮点数范围越大,但精度下降
- 左规:尾数左移1位,阶码减1(r=2)
- 右规:尾数右移1位,阶码加1(r=2)
- 机器零
- 浮点数尾数为0,无论阶码为何值;
- 阶码小于或等于它所能表示的最小数时
- 阶码用移码表示,尾数用补码表示,则机器零为0000···0000
IEEE 754 标准
S 阶码(含阶符) 尾数 - 阶码存在一个偏移量
- 尾数的整数位1被省略,称为隐藏位(对于短实数和长实数而言)
浮点数类型 符号位S 阶码 尾数 总位数 短实数 1 8 23 32 长实数 1 11 52 64 临时实数 1 15 64 80
3.3 定点运算
移位运算
移位与加减配合,能够实现乘除运算
- 算术移位
- 有符号数的移位
移位规则
真值 码制 添补代码 正数 原码、补码、反码 0 负数 原码 0 负数 补码 左移添0
右移添1负数 反码 1 移位结果
真值 码制 左移 右移 正数 原码、补码、反码 最高位丢1,结果出错 最低位丢1,影响精度 负数 原码 最高位丢1,结果出错 最低位丢1,影响精度 负数 补码 最高位丢0,结果出错 最低位丢1,影响精度 负数 反码 最高位丢0,结果出错 最低位丢0,影响精度
- 逻辑移位
- 无符号数的移位
- 左移:高位移丢,低位添0
- 右移:低位移丢,高位添0
加减法运算
- 补码加减运算公式
- 加法
- 整数:$[A]_补+[B]_补=[A+B]_补(mod 2^{n+1})$
- 小数:$[A]_补+[B]_补=[A+B]_补(mod 2)$
- 减法
- $A-B=A+(-B)$
- 连同符号位一起相加,符号位产生的进位自然丢掉
- 加法
- 溢出判断
- 一位符号位判断溢出
- 参加操作的两个数符号相同,但其结果的符号与原操作数的符号不同,即为溢出
- 两位符号位判断溢出
- 采用变形补码 \([x]_{补^{'}} =\begin{cases} x & 1>x \geq 0 \\ 4+x & 0 > x \geq -1 \end{cases}\)
- 化成变形补码进行加减运算,包括两个符号位 - 双符号位相同:未溢出 - 双符号位不同:溢出 - 最高符号位代表真正的符号
- 一位符号位判断溢出
乘法运算
- 一般乘法规则(一位乘)
- 通过加和移位实现(位数为n):加n次,移n次
- 由乘数的末位决定被乘数是否与原部分积相加,然后结果»1形成新的部分积,同时乘数»1(末位移丢),空出高位存放部分积的低位
- 被乘数只与部分积的高位相加
- 硬件:3个寄存器,具有移位功能;1个全加器
- 原码乘法
- 乘积的符号位单独处理:$x_0 \bigoplus y_0$
- 数值部分为绝对值相乘$x^* · y^*$
- 用移位的次数判断乘法是否结束
- 逻辑移位(因为是绝对值)
- 补码乘法 $[x]_补=x_0.x_1x_2···x_n$ $[y]_补=y_0.y_1y_2···y_n$
- 被乘数任意,乘数为正
- $[x·y]_补 = [x]_补 · [y]_补 = [x]_补·y$
- 同原码乘的规则类似,但是加和移位按补码规则运算,乘积的符号自然形成
- 被乘数任意,乘数为负(校正法)
- $[x·y]_补 = [x]_补(0.y_1y_2···y_n) + [-x]_补$
- Booth算法(被乘数、乘数符号任意)
又称:比较法
- $[x·y]_补 = [x]_补(0.y_1y_2···y_n) - [x]_补·y_0$
- $[x·y]补 = [x]_补[(y_1-y_0)+(y_2-y_1)2^{-1}+···+(y{n+1}-y_n)2^{-n}]$
其中,$y_{n+1}=0$ - 最后一步不移位
- 部分积取双符号位,乘数多取一位(因为符号位参与运算)
- 被乘数任意,乘数为正
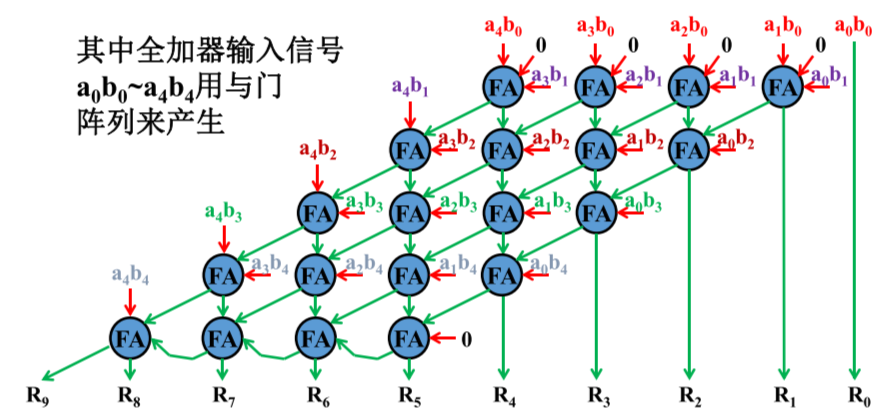
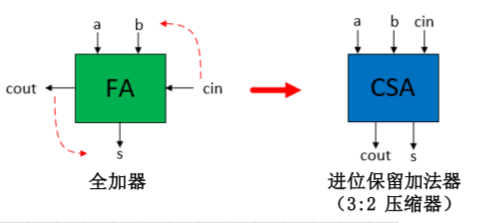
- 快速乘法器
除法运算
- 一般规则
- 符号位异或形成
$ x - y >0$ 上商1
$x - y <0$ 上商0 - 余数左移一位,低位补“0”
- 在寄存器最末位上商
- 原码除法
- 约定:小数定点除法$x^<y^$;整数定点除法$x^>y^$;被除数和除数不能为0
- 恢复余数法
- 当余数为负时,需加上除数,将其恢复成原来的余数
- 第一次上商判断溢出
- 加减交替法(不恢复余数法)
- 余数$R_i>0$,上商“$1$”,$2R_i-y$
- 余数$R_i<0$,上商“$0$”,$2R_i+y$
- n位小数的除法上商n次,左移n次(移位的次数判断是否结束)
4.4 浮点四则运算
浮点加减运算
- 对阶
- 小阶向大阶看齐
- 尾数求和
- 规格化
- |编码|解释| |:–:|:–:| |原码|不论正数、负数,第一数位为1| |补码|符号位和第一数位不同| 补码特例:$[-1/2]_补$不是规格化的数;$[-1]_补$是规格化的数
- 左规:尾数左移一位,阶码减1,直到数符和第一数位不同为止
- 右规:尾数溢出,需右规
- 舍入
- 在对阶和右规过程中,可能出现尾数末位丢失,引起误差,需考虑舍入
- 0舍1入法:移去的末位为0,则舍去;移去的末位为1,则在尾数的末位加1
- 恒置1法:末位恒置1
- 溢出判断
- 由阶码符号决定
浮点乘除运算
- 乘法
- 阶码相加:需要进行溢出判断
- 尾数相乘:按定点乘法运算方法
- 规格化
- 除法
- 尾数调整:若被除数尾数大于除数尾数(绝对值),则将被除数尾数右移一位,阶码+1
- 阶码相减
- 尾数相除
3.5 算术逻辑单元
ALU电路
- 组合逻辑电路,能完成算术运算和逻辑运算
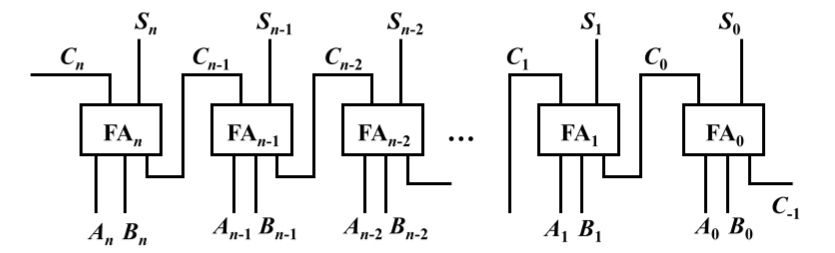
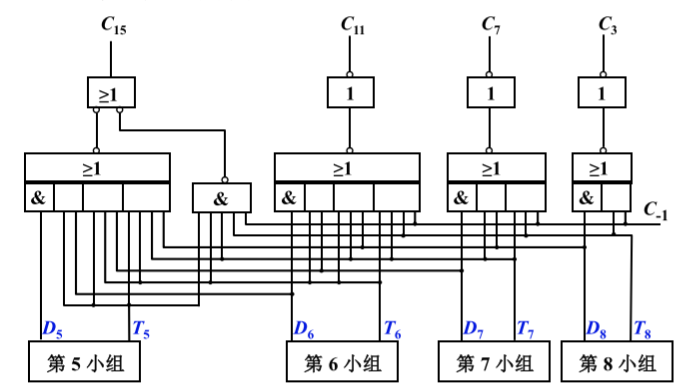
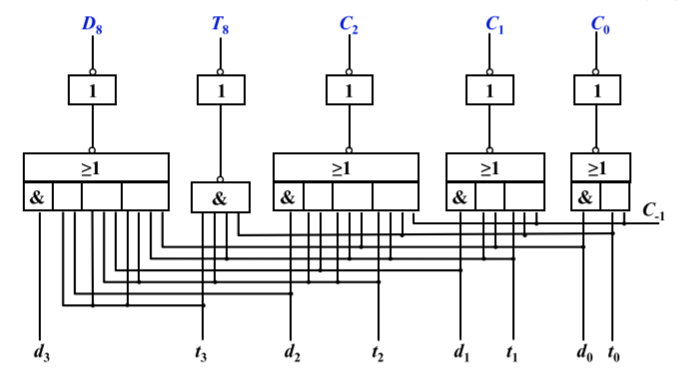
快速进位链
This post is licensed under CC BY 4.0 by the author.